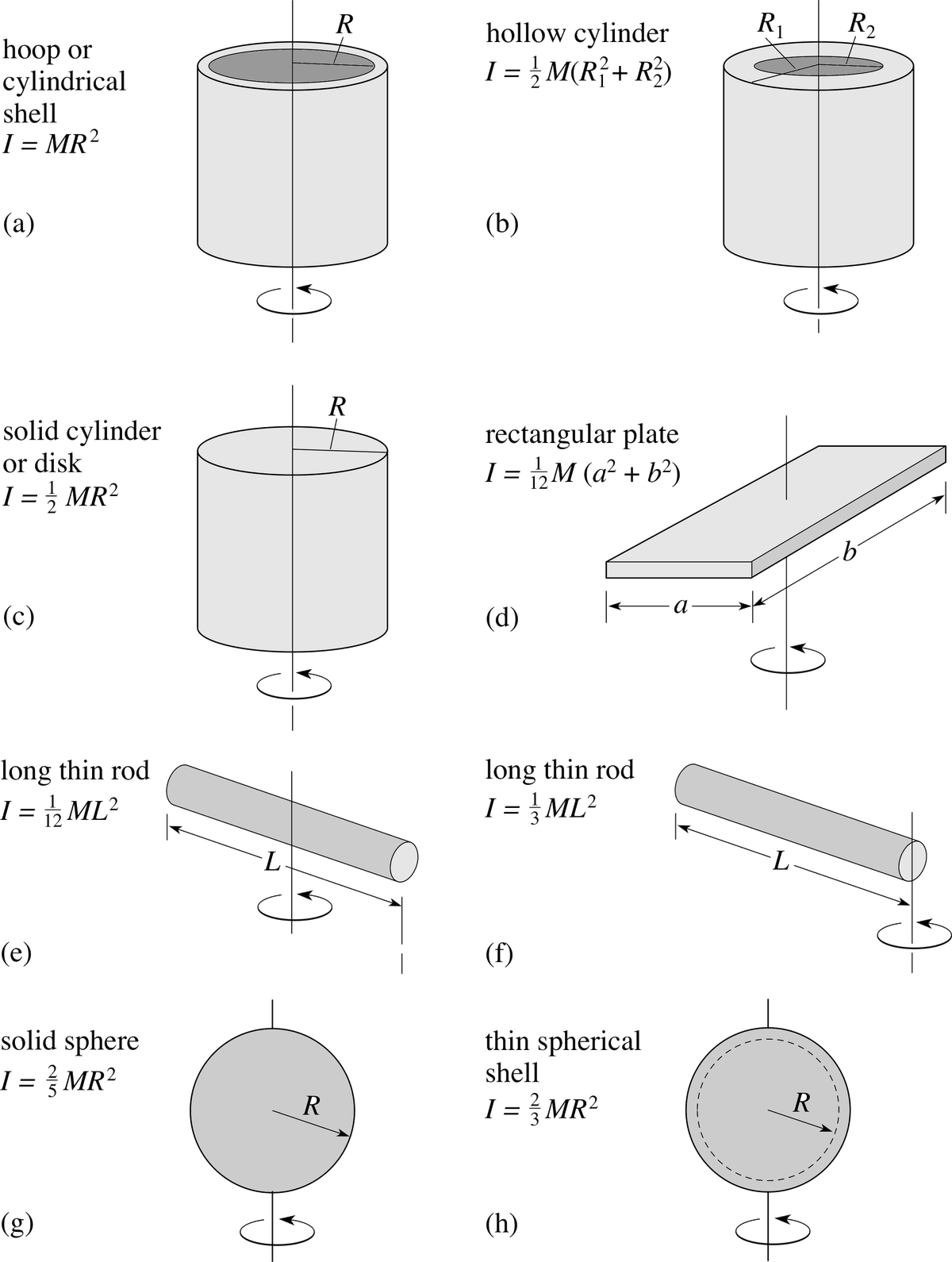
Where the planar second moment of area describes an object's resistance to deflection (bending) when subjected to a force applied to a plane parallel to the central axis, the polar second moment of area describes an object's resistance to deflection when subjected to a moment applied in a plane perpendicular to the object's central axis (i.e. It is a constituent of the second moment of area, linked through the perpendicular axis theorem. Here the free polar moment of inertia calculator also shows the same results. The polar moment (of inertia), also known as second (polar) moment of area, is a quantity used to describe resistance to torsional deformation (deflection), in cylindrical (or non-cylindrical) objects (or segments of an object) with an invariant cross-section and no significant warping or out-of-plane deformation. In following sections we will use the integral definitions of moment of inertia to find the moments of inertia of five common shapes: rectangle, triangle, circle, semi-circle, and quarter-circle with respect to a specified axis. Free line equation calculator - find the equation of a line step-by-step.